18. Beep! GBA sound introduction
Introduction to GBA sound
Apart from graphics and interaction, there is one other sense important to games: audio. While graphics may set the scene, sound sets the mood, which can be even more important that the graphics. Try playing Resident Evil with, say, “Weird Al” Yankovic playing: it simply doesn’t work, the atmosphere is lost.
The GBA has six sound channels. The first four are roughly the same as the original Game Boy had: two square wave generators (channels 1 and 2), a sample player (channel 3) and a noise generator (channel 4). Those are also referred to as the DMG channels after the Game Boy’s code name “Dot Matrix Game.” New are two Direct Sound channels A and B (not to be confused with Microsoft’s DirectSound, the DirectX component). These are 8-bit digital pulse code modulation (PCM) channels.
I should point out that I really know very little about sound programming, mostly because I’m not able to actually put together a piece of music (it’s kinda hard to do that when you already have music playing). If you want to really learn about sound programming, you should look at Belogic.com, where almost everybody got their information from, and deku.gbadev.org, which shows you how to build a sound mixer. Both of these sites are excellent.
I may not know much about sound creation/programming, but at its core sound is a wave in matter; waves are mathematical critters, and I do know a thing or two about math, and that’s kind of what I’ll do here for the square wave generators.
Sound and Waves
Consider if you will, a massive sea of particles, all connected to their neighbours with little springs. Now give one of them a little push. In the direction of the push, the spring compresses and relaxes, pushing the original particle back to its normal position and passing on the push to the neighbour; this compresses the next spring and relays the push to its neighbour, and so on and so on.
This is a prime example of wave behaviour. Giving a precise definition of a wave that covers all cases is tricky, but in essence, a wave is a transferred disturbance. There are many kinds of waves; two major classes are longitudinal waves, which oscillate in the direction of travel, and transverse waves, which are perpendicular to it. Some waves are periodic (repeating patterns over time or space), some aren’t. Some travel, some don’t.
Waves
The canonical wave is the harmonic wave. This is any function ψ(x) that’s a solution to eq 18.1. The name of the variable doesn’t really matter, but usually it’s either spatial (x, y, z) or temporal (t), or all of these at the same time. The general solution can be found in eq 18.2. Or perhaps I should say solutions, as there are many ways of writing them down. They’re all equivalent though, and you can go from one to the other with some trickery that does not concern us at this moment.
| (18.1) |
General solution(s):
| (18.2) |
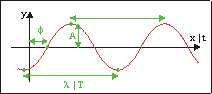
Fig 18.1: a harmonic wave
A full wave can be described by three things. First, there’s the amplitude A, which gives half-distance between the minimum and maximum. Second, the wavelength λ, which is the length after which the wave repeats itself (this is tied to wave-number k= 2π/λ). Then there’s phase constant φ0, which defines the stating point. If the wave is in time, instead of a wavelength you have period T, frequency f=1/T (and angular frequency ω= 2πf= 2π/T). You can see what each of these parameters is in fig 18.1.
One of the interesting things about the wave equation is that it is a linear operation on ψ. What that means is that any combination of solutions is also a solution; this is the superposition principle. For example, if you have two waves ψ1 and ψ2, then Ψ = aψ1 + bψ2 is also a wave. This may sound like a trivial thing but I assure you it’s not. The fact that non-linear equations (and they exist too) tend to make scientists cringe a little should tell you something about the value of linear equations.
Sound waves
Sound is also a wave. In fact, it is a longitudinal pressure wave in matter and pretty much works as the system of particles on springs mentioned earlier with whole sets of molecules moving back and forth. In principle, it has both spatial and temporal structure, and things can get hideously complex if you want to deal with everything. But I’ll keep it easy and only consider two parts: amplitude A and period and frequency T and f. As you probably know, the tone of a sound is related to the frequency. Human hearing has a range between 20 Hz and 20 kHz, and the higher the frequency (that is, the more compressed the wave), the higher the tone. Most sounds are actually a conglomeration of different waves, with different amplitudes and frequencies – the superposition principle at work. The funny thing about this is that if you added all those components up to one single function and plot it, it wouldn’t look like a sine wave at all anymore. What’s even funnier is that you can also reverse the process and take a function –any function– and break it up into a superposition of sine and cosine waves, and so see what kind of frequencies your sound has. This is called Fourier Transformation, and we’ll get to that in a minute.
Musical scale
While the full range between 20 Hz and 20 kHz is audible, only a discrete set of frequencies are used for music, which brings us to the notion of the musical scale. Central to these are octaves, representing a frequency doubling. Each octave is divided into a number of different notes; 12 in Western systems, ranging from A to G, although octave numbering starts at C for some reason. Octave 0 starts at the central C, which has a frequency of about 262 Hz (see also table 18.1. And yes, I know there are only 7 letters between A and G, the other notes are flats and sharps that lie between these notes. The ‘12’ refers to the number of half-notes in an octave. The musical scale is logarithmic; each half-note being 21/12 apart. Well, almost anyway: for some reason, some notes don’t quite fit in exactly.
| half-note | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| name | C | C# | D | D# | E | F | F# | G | G# | A | A# | B | (C) |
| freq (Hz) | 261.7 | 277.2 | 293.7 | 311.2 | 329.7 | 349.3 | 370.0 | 392.0 | 415.3 | 440.0 | 466.2 | 493.9 | (523.3) |
Fourier transforms and the square wave
Fourier transformations are a way of describing a function in the time domain as a distribution of frequencies called a spectrum. They’re also one of the many ways that professors can scare the bejebus out of young, natural-science students. Don’t worry, I’m sure you’ll get through this section unscathed >:). For well - to reasonably - behaved functions, you can rewrite them as series of very well-behaved functions such as polynomials, exponentials and also waves. For example, as a Fourier series, a function may look like eq 18.3.
| (18.3) |
Of course, the whole thing relies on being able to find the coefficients Am and Bm. While it is fairly straightforward to derive the equations for them, I’ll leave that as an exercise for the reader and just present the results in the form of eq 18.4. I should mention that there are actually a few ways of defining Fourier transforms. For example, there are versions that don’t integrate over [0,T], but over [−½T, ½T]; or use the complex exponential instead of sines and cosines, but in the end they’re all doing the same thing.
| (18.4) |
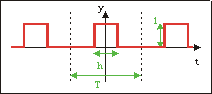
Fig 18.2: a square wave
As an example, let’s take a look at the square wave shown in fig 18.2. A square wave is on (1) for a certain time (parameter h), then off (0) for the rest of the cycle. It’s still a periodic wave, so it doesn’t really matter where we place the thing along the t-axis. I centered it on the peak for convenience: doing so makes it a symmetrical wave which has the nice properly of removing all the anti-symmetrical sine waves. A0=h/T because it’s the average of the function and the rest of the Am’s follow from eq 18.4.
| (18.5) |
Am is a sinc function: sin(x)/x. For high m it approaches zero (as it should, since higher terms should be relatively less important), but also interesting is that of the higher terms some will also vanish because of the sine. This will happen whenever m is a multiple of T/h.
GBA sound
Sound registers
For graphics, you only had to deal with two registers (REG_DISPCNT and REG_BGxCNT) to get a result; for sound, you have to cover a lot of registers before you get anything. The DMG channels each have 2 or 3 registers – some with similar functionality, some not. Apart from that, there are four overall control registers.
The register nomenclature seems particularly vexed when it comes to sound. There are basically two sets of names that you can find: one consisting of REG_SOUNDxCNT followed by _L, _H and _X in a rather haphazard manner; the other one uses a REG_SGxy and REG_SGCNTy structure (x=1, 2, 3 or 4 and y=0 or 1). I think the former is the newer version, which is funny because the older is more consistent. Oh well. In any case, I find neither of them very descriptive and keep forgetting which of the L/H/X or 0/1 versions does what, so I use a third set of names based on the ones found in tepples’ pin8gba.h, which IMHO makes more sense than the other two.
| offset | function | old | new | tonc |
|---|---|---|---|---|
| 60h | channel 1 (sqr) sweep | REG_SG10 | SOUND1CNT_L | REG_SND1SWEEP |
| 62h | channel 1 (sqr) len, duty, env | SOUND1CNT_H | REG_SND1CNT | |
| 64h | channel 1 (sqr) freq, on | REG_SG11 | SOUND1CNT_X | REG_SND1FREQ |
| 68h | channel 2 (sqr) len, duty, env | REG_SG20 | SOUND2CNT_L | REG_SND2CNT |
| 6Ch | channel 2 (sqr) freq, on | REG_SG21 | SOUND2CNT_H | REG_SND2FREQ |
| 70h | channel 3 (wave) mode | REG_SG30 | SOUND3CNT_L | REG_SND3SEL |
| 72h | channel 3 (wave) len, vol | SOUND3CNT_H | REG_SND3CNT | |
| 74h | channel 3 (wave) freq, on | REG_SG31 | SOUND3CNT_X | REG_SND3FREQ |
| 78h | channel 4 (noise) len, vol, env | REG_SG40 | SOUND4CNT_L | REG_SND4CNT |
| 7Ch | channel 4 (noise) freq, on | REG_SG41 | SOUND4CNT_H | REG_SND4FREQ |
| 80h | DMG master control | REG_SGCNT0 | SOUNDCNT_L | REG_SNDDMGCNT |
| 82h | DSound master control | SOUNDCNT_H | REG_SNDDSCNT | |
| 84h | sound status | REG_SGCNT1 | SOUNDCNT_X | REG_SNDSTAT |
| 88h | bias control | REG_SGBIAS | SOUNDBIAS | REG_SNDBIAS |
“Oh great. This is going to be one of ‘tegel’ things isn’t it? Where you think you’ve got something nice but different going, then later you revert to the standard terminology to conform with the rest of the world. Right?”
No, I’ll stick to these names. Probably. Hopefully. … To be honest, I really don’t know :P. This is not really a big deal, though: you can easily switch between names with a few defines or search & replaces. Anyway, REG_SNDxFREQ contains frequency information and REG_SNDxCNT things like volume and envelope settings; in some cases, the bit layouts are even exactly the same. Apart from the sweep function of channel 1, it is exactly the same as channel 2.
Master sound registers
REG_SNDDMGCNT, REG_SNDDSCNT and REG_SNDSTAT are the master sound controls; you have to set at least some bits on each of these to get anything to work.
| F | E | D | C | B | A | 9 | 8 | 7 | 6 5 4 | 3 | 2 1 0 |
| R4 | R3 | R2 | R1 | L4 | L3 | L2 | L1 | - | RV | - | LV |
| bits | name | define | description |
|---|---|---|---|
| 0-2 | LV | Left volume | |
| 4-6 | RV | Right volume | |
| 8-B | L1-L4 | SDMG_LSQR1, SDMG_LSQR2, SDMG_LWAVE, SDMG_LNOISE | Channels 1-4 on left |
| C-F | R1-R4 | SDMG_RSQR1, SDMG_RSQR2, SDMG_RWAVE, SDMG_RNOISE | Channels 1-4 on right |
REG_SNDDMGCNT controls the main volume of the DMG channels and which ones are enabled. These controls are separate for the left and right speakers. Below are two macros that make manipulating the register easier. Note that they don’t actually set the register, just combine the flags.
#define SDMG_SQR1 0x01
#define SDMG_SQR2 0x02
#define SDMG_WAVE 0x04
#define SDMG_NOISE 0x08
#define SDMG_BUILD(_lmode, _rmode, _lvol, _rvol) \
( ((_lvol)&7) | (((_rvol)&7)<<4) | ((_lmode)<<8) | ((_rmode)<<12) )
#define SDMG_BUILD_LR(_mode, _vol) SDMG_BUILD(_mode, _mode, _vol, _vol)
| F | E | D | C | B | A | 9 | 8 | 7 6 5 4 | 3 | 2 | 1 0 |
| BF | BT | BL | BR | AF | AT | AL | AR | - | BV | AV | DMGV |
| bits | name | define | description |
|---|---|---|---|
| 0-1 | DMGV | SDS_DMG25, SDS_DMG50, SDS_DMG100 | DMG Volume ratio.
|
| 2 | AV | SDS_A50, SDS_A100 | DSound A volume ratio. 50% if clear; 100% of set |
| 3 | BV | SDS_B50, SDS_B100 | DSound B volume ratio. 50% if clear; 100% of set |
| 8-9 | AR, AL | SDS_AR, SDS_AL | DSound A enable Enable DS A on right and left speakers |
| A | AT | SDS_ATMR0, SDS_ATMR1 | Dsound A timer. Use timer 0 (if clear) or 1 (if set) for DS A |
| B | AF | SDS_ARESET | FIFO reset for Dsound A. When using DMA for Direct sound, this will cause DMA to reset the FIFO buffer after it's used. |
| C-F | BR, BL, BT, BF | SDS_BR, SDS_BL, SDS_BTMR0, SDS_BTMR1, SDS_BRESET | As bits 8-B, but for DSound B |
Don’t know too much about REG_SNDDSCNT, apart from that it governs PCM sound, but also has some DMG sound bits for some reason. REG_SNDSTAT shows the status of the DMG channels and enables all sound. If you want to have any sound at all, you need to set bit 7 there.
| F E D C B A 9 8 | 7 | 6 5 4 | 3 | 2 | 1 | 0 |
| - | MSE | - | 4A | 3A | 2A | 1A |
| bits | name | define | description |
|---|---|---|---|
| 0-3 | 1A-4A | SSTAT_SQR1, SSTAT_SQR2, SSTAT_WAVE, SSTAT_NOISE | Active channels. Indicates which DMG channels are
currently playing. They do not enable the channels;
that's what REG_SNDDMGCNT is for.
|
| 7 | MSE | SSTAT_DISABLE, SSTAT_ENABLE | Master Sound Enable. Must be set if any sound is to be heard at all. Set this before you do anything else: the other registers can't be accessed otherwise, see GBATEK for details. |
Sound register access
Emulators may allow access to sound registers even if sound is disabled (REG_SNDSTAT{7} is clear), but hardware doesn’t. Always enable sound before use.
GBA Square wave generators
The GBA has two square sound generators, channels 1 and 2. The only difference between them is channel 1’s frequency sweep, which can make the frequency rise or drop exponentially as it’s played. That’s all done with REG_SND1SWEEP. REG_SNDxCNT controls the wave’s length, envelope and duty cycle. Length should be obvious. The envelope is basically the amplitude as function of time: you can make it fade in (attack), remain at the same level (sustain) and fade out again (decay). The envelope has 16 volume levels and you can control the starting volume, direction of the envelope and the time till the next change. Volumes are linear: 12 produces twice the amplitude of 6. The duty refers to the ratio of the ‘on’ time and the period, in other words D = h/T.
Of course, you can control the frequency as well, namely with REG_SNDxFREQ. However, it isn’t the frequency that you enter in this field. It’s not exactly the period either; it’s something I’ll refer to as the rate R. The three quantities are related, but different in subtle ways and chaos ensues when they’re confused – and they often are in documentation, so be careful. The relation between frequency f and rate R is described by eq 18.6; if the rate goes up, so does the frequency. Since R ∈ [0, 2047], the range of frequencies is [64 Hz, 131 kHz]. While this spans ten octaves, the highest ones aren’t of much use because the frequency steps become too large (the denominator in eq eq 18.6 approaches 0).
| (18.6a) | |
| (18.6b) |
Square sound registers
Both square-wave generators have registers REG_SNDxCNT for envelope/length/duty control and REG_SNDxFREQ for frequency control. Sound 1 also has sweep control in the form of REG_SND1SWEEP. Look in table 18.2 for the traditional names; note that in traditional nomenclature the suffixes for control and frequency are different for channels 1 and 2, even though they have exactly the same function.
| F E D C | B | A 9 8 | 7 6 | 5 4 3 2 1 0 |
| EIV | ED | EST | D | L |
| bits | name | define | description |
|---|---|---|---|
| 0-5 | L | SSQR_LEN# | Sound Length. This is a write-only field and only
works if the channel is timed (REG_SNDxFREQ{E}). The
length itself is actually (64−L)/256 seconds for a
[3.9, 250] ms range.
|
| 6-7 | D | SSQR_DUTY1_8, SSQR_DUTY1_4, SSQR_DUTY1_2, SSQR_DUTY3_4, SSQR_DUTY# | Wave duty cycle. Ratio between on and of times of the square wave. Looking back at eq 18.2, this comes down to D=h/T. The available cycles are 12.5%, 25%, 50%, and 75% (one eighth, quarter, half and three quarters). |
| 8-A | EST | SSQR_TIME# | Envelope step-time. Time between envelope changes: Δt = EST/64 s. |
| B | ED | SSQR_DEC, SSQR_INC | Envelope direction. Indicates if the envelope decreases (default) or increases with each step. |
| C-F | EIV | SSQR_IVOL# | Envelope initial value. Can be considered a volume
setting of sorts: 0 is silent and 15 is full volume. Combined
with the direction, you can have fade-in and fade-outs; to have a
sustaining sound, set initial volume to 15 and an increasing
direction. To vary the real volume, remember
REG_SNDDMGCNT.
|
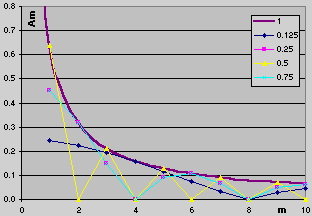
Fig 18.3: Square wave spectrum. (integer m only)
Some more on the duty cycle. Remember we’ve done a Fourier analysis of the square wave so we could determine the frequencies in it. Apart from the base frequency, there are also overtones of frequencies m·f. The spectrum (see fig 18.3) gives the amplitudes of all these frequencies. Note that even though the figure has lines, only integral values of m are allowed. The base frequency at m=1 has the highest significance and the rest falls off with 1/m. The interesting part is when the sine comes into play: whenever m·D is an integer, that component vanishes! With a fractional duty number –like the ones we have– this happens every time m is equal to the denominator. For the 50% duty, every second overtone disappears, leaving a fairly smooth tone; for 12.5%, only every eighth vanishes and the result is indeed a noisier sound. Note that for both ¼ and ¾ duties every fourth vanishes so that they should be indistinguishable. I was a little surprised about this result, but sure enough, when I checked they really did sound the same to me.
| F | E | D C B | A 9 8 7 6 5 4 3 2 1 0 |
| Re | T | - | R |
| bits | name | define | description |
|---|---|---|---|
| 0-A | R | SFREQ_RATE# | Sound rate. Well, initial rate. That's rate, not frequency. Nor period. The relation between rate and frequency is f = 217/(2048-R). Write-only field. |
| E | T | SFREQ_HOLD, SFREQ_TIMED | Timed flag. If set, the sound plays for as long as
the length field (REG_SNDxCNT{0-5}) indicates.
If clear, the sound plays forever. Note that even if a decaying
envelope has reached 0, the sound itself would still be considered
on, even if it's silent.
|
| F | Re | SFREQ_RESET | Sound reset. Resets the sound to the initial volume (and
sweep) settings. Remember that the rate field is in this register
as well and due to its write-only nature a simple
‘|= SFREQ_RESET’ will not suffice
(even though it might on emulators).
|
| F E D C B A 9 8 7 | 6 5 4 | 3 | 2 1 0 |
| - | T | M | N |
| bits | name | define | description |
|---|---|---|---|
| 0-2 | N | SSW_SHIFT# | Sweep number. Not the number of sweeps; see the discussion below. |
| 3 | M | SSW_INC, SSW_DEC | Sweep mode. The sweep can take the rate either up (default) or down (if set). |
| 4-6 | T | SSW_TIME# | Sweep step-time. The time between sweeps is measured in 128 Hz (not kHz!): Δt = T/128 ms ≈ 7.8T ms; if T=0, the sweep is disabled. |
I’m reasonably confident that the exact workings of shifts are explained without due care in most documents, so here are a few more things about it. Sure enough, the sweep does make the pitch go up or down which is controlled by bit 3, and the step-time does change the pitch after that time, but exactly what the sweep-shift does is ambiguous at best. The information is in there, but only if you know what to look for. The usual formula given is something like:
That’s what belogic gives and if you know what the terms are you’ll be fine. Contrary to what you may read, the sweep does not apply to the frequency (f). It does not apply to the period (T, see above). It applies to the rate (R). If you look in emulators, you can actually see the rate-value change.
Second, the n in the exponent is not the current sweep index that runs up to the number of sweep shifts. It is in fact simply the sweep shift number, and the sweeps continue until the rate reaches 0 or the maximum of 2047.
The formulas you may see do say that, but it’s easy to misread them. I did. Eq 18.7 holds a number of correct relations. R is the rate, n is the sweep shift (18.7c explains why it’s called a shift (singular, not plural)), and j is the current sweep index. You can view them in a number of ways, but they all boil down to exponential functions, that’s what ‘dy*(x) = a·y(x)dx*’ means, after all. For example, if n=1, then you get 1½j and ½j behaviour for increasing and decreasing sweeps, respectively; with n=2 it’s 1¼j and ¾j, etc. The higher the shift, the slower the sweep.
| (18.7a) |
| (18.7b) |
| (18.7c) |
R += R >> n;
|
Playing notes
Even though the rates are equal, some may be considered more equal than others. I’ve already given a table with the frequencies for the standard notes (table 18.1) of octave 0. You can of course convert those to rates via eq 18.6b and use them as such. However, it might pay to figure out how to play the notes of all octaves.
To do this, we’ll use some facts I mentioned in section 18.2.3. about the make-up of the musical scale. While I could make use of the logarithmic relation between successive notes (Δf=21/12·f), I’ll restrict myself to the fact that notes between octaves differ by a factor of two. We’ll also need the rate-frequency relation (obviously). That’s the basic information you need, I’ll explain more once we get through all the math. Yes, it’s more math, but it’ll be the last of this page, I promise.
The equations we’ll start with are the general frequency equation and the rate-frequency relation. In these we have rate R, frequency f and octave c. We also have a base octave C and frequency F in that base octave.
And now for the magic. And you are expected to understand this.
| (18.8) |
Right, and now for why this thing’s useful. Remember that the GBA has no hardware division or floating-point support, so we’re left with integers and (if possible) shifts. That’s why the last term in the last step of eq 18.8 was separated. The term with F gives a rate offset for the base octave, which we need to divide (read: shift) by the octave offset term for the different octaves. Remember that integer division truncates, so we need a big numerator for the most accuracy. This can be done with a large C and by adding an extra term m. Basically, this makes it an mf fixed point division. The workable octave range is −2 to 5, so we take C=5. The value for m is almost arbitrary, but needs to be higher than two because of the minimum octave is −2, and a shift can never be negative. m=4 will suffice.
Note that there is still a division in there. Fortunately, there are only twelve values available for F, so might just as well store the whole term in a look-up table. The final result is listing 18.1 below.
// Listing 18.1: a sound-rate macro and friends
typedef enum
{
NOTE_C=0, NOTE_CIS, NOTE_D, NOTE_DIS,
NOTE_E, NOTE_F, NOTE_FIS, NOTE_G,
NOTE_GIS, NOTE_A, NOTE_BES, NOTE_B
} eSndNoteId;
// Rates for equal temperament notes in octave +5
const u32 __snd_rates[12]=
{
8013, 7566, 7144, 6742, // C , C#, D , D#
6362, 6005, 5666, 5346, // E , F , F#, G
5048, 4766, 4499, 4246 // G#, A , A#, B
};
#define SND_RATE(note, oct) ( 2048-(__snd_rates[note]>>(4+(oct))) )
// sample use: note A, octave 0
REG_SND1FREQ= SFREQ_RESET | SND_RATE(NOTE_A, 0);
Here you have a couple of constants for the note-indices, the LUT with rate-offsets __snd_rates and a simple macro that gives you what you want. While __snd_rates is constant here, you may consider a non-const version to allow tuning. Not that a square wave is anything worth tuning, but I’m just saying … y’know.
One possible annoyance is that you have to splice the note into a note and octave part and to do that dynamically you’d need division and modulo by 12. Or do you? If you knew a few things about division by a constant is multiplication by its reciprocal, you’d know what to do. (Hint: c=(N*43>>9)−2, where N is the total note index between 0 and 95 (octave −2 to +5).)
Demo time
I think I’ve done about enough theory for today; don’t you, dear reader?
“ @_@ ”
I’ll take that as a yes. The demo in question demonstrates the use of the various macros of this chapter, most notably SND_RATE. It also shows how you can play a little song – and I use the term lightly – with the square wave generator. I hope you can recognize which one.
#include <stdio.h>
#include <tonc.h>
u8 txt_scrolly= 8;
const char *names[]=
{ "C ", "C#", "D ", "D#", "E ", "F ", "F#", "G ", "G#", "A ", "A#", "B " };
// === FUNCTIONS ======================================================
// Show the octave the next note will be in
void note_prep(int octave)
{
char str[32];
siprintf(str, "[ %+2d]", octave);
se_puts(8, txt_scrolly, str, 0x1000);
}
// Play a note and show which one was played
void note_play(int note, int octave)
{
char str[32];
// Clear next top and current rows
SBB_CLEAR_ROW(31, (txt_scrolly/8-2)&31);
SBB_CLEAR_ROW(31, txt_scrolly/8);
// Display note and scroll
siprintf(str, "%02s%+2d", names[note], octave);
se_puts(16, txt_scrolly, str, 0);
txt_scrolly -= 8;
REG_BG0VOFS= txt_scrolly-8;
// Play the actual note
REG_SND1FREQ = SFREQ_RESET | SND_RATE(note, octave);
}
// Play a little ditty
void sos()
{
const u8 lens[6]= { 1,1,4, 1,1,4 };
const u8 notes[6]= { 0x02, 0x05, 0x12, 0x02, 0x05, 0x12 };
int ii;
for(ii=0; ii<6; ii++)
{
note_play(notes[ii]&15, notes[ii]>>4);
VBlankIntrDelay(8*lens[ii]);
}
}
int main()
{
REG_DISPCNT= DCNT_MODE0 | DCNT_BG0;
irq_init(NULL);
irq_add(II_VBLANK, NULL);
txt_init_std();
txt_init_se(0, BG_CBB(0) | BG_SBB(31), 0, CLR_ORANGE, 0);
pal_bg_mem[0x11]= CLR_GREEN;
int octave= 0;
// turn sound on
REG_SNDSTAT= SSTAT_ENABLE;
// snd1 on left/right ; both full volume
REG_SNDDMGCNT = SDMG_BUILD_LR(SDMG_SQR1, 7);
// DMG ratio to 100%
REG_SNDDSCNT= SDS_DMG100;
// no sweep
REG_SND1SWEEP= SSW_OFF;
// envelope: vol=12, decay, max step time (7) ; 50% duty
REG_SND1CNT= SSQR_ENV_BUILD(12, 0, 7) | SSQR_DUTY1_2;
REG_SND1FREQ= 0;
sos();
while(1)
{
VBlankIntrWait();
key_poll();
// Change octave:
octave += bit_tribool(key_hit(-1), KI_R, KI_L);
octave= wrap(octave, -2, 6);
note_prep(octave);
// Play note
if(key_hit(KEY_DIR|KEY_A))
{
if(key_hit(KEY_UP))
note_play(NOTE_D, octave+1);
if(key_hit(KEY_LEFT))
note_play(NOTE_B, octave);
if(key_hit(KEY_RIGHT))
note_play(NOTE_A, octave);
if(key_hit(KEY_DOWN))
note_play(NOTE_F, octave);
if(key_hit(KEY_A))
note_play(NOTE_D, octave);
}
// Play ditty
if(key_hit(KEY_B))
sos();
}
return 0;
}
The bolded code in main() initializes the sound register; nothing fancy, but it has to be done before you hear anything at all. It is important to start with REG_SNDSTAT bit 7 (SSTAT_ENABLE), i.e., the master sound enable. Without it, you cannot even access the other registers. Setting volume to something non-zero is a good idea too, of course. Then we turn off the sweep function and set sound 1 to use a fading envelope with a 50% duty. And that’s where the fun starts.
I’ll explain what sos() is in a little while; but first, something about the controls of the demo. You can play notes with the D-pad and A (hmm, there’s something familiar about that arrangement). The octave c you’re working in can be changed with L and R; the background color changes with it. B plays sos() again.
| A / D-pad | Play a note |
|---|---|
| ↑ : D (next octave) | |
| ← : B | |
| → : A | |
| ↓ : F | |
| A : D | |
| L / R | Decrease / Increase current octave ([-2, 5], wraps around) |
| B | Play a little tune. |
The D-pad and A select a note to play, which is handled by note_play(). The bolded line there plays the actual note, the rest is extra stuff that writes the note just played to the screen and scrolls along so you can see the history of what’s been played. The code for this is kinda ugly, but is not exactly central to the story so that’s fine.
Playing a little ditty
So what is sos() all about then? Let’s take another look.
void sos()
{
const u8 lens[6]= { 1,1,4, 1,1,4 };
const u8 notes[6]= { 0x02, 0x05, 0x12, 0x02, 0x05, 0x12 };
int ii;
for(ii=0; ii<6; ii++)
{
note_play(notes[ii]&15, notes[ii]>>4);
VBlankIntrDelay(8*lens[ii]);
}
}
There are two arrays here, notes and lens, and a loop over all elements. We take a byte from notes and use the nybbles for octave and note information, play the note, then wait a while –the length is indicated by the lens array– before the next note is played. Basically, we’re playing music. Hey, if the likes of Schnappi and Crazy Frog can make it into the top 10, I think I’m allowed to call this music too, alright? Alright.
The point I’m trying to make is that it’s very well possible to play a tune with just the tone generators. Technically you don’t need digitized music and all that stuff to play something. Of course, it’ll sound better if you do, but if you just need a little jingle the tone generators may be all you need. Twelve years of Game Boy games using only tone generators prove this. Just define some notes (the nybble format for octaves and notes will do) and some lengths and you have the basics already. You could even use more than one channel for different effects.
If you understood that, then get this: the note+length+channel idea is pretty much what tracked music (mod, it, xm, etc) does, only that they use a more sophisticated wave than a square wave. But the principle is the same. Getting it to work takes a little more effort, but that’s what Deku’s sound mix tutorial is for.